About

FROSch (Fast and Robust Overlapping Schwarz) is a Framework for parallel Schwarz preconditioners in Trilinos. It is part of the package Trilinos package ShyLU.

In particular, FROSch provides preconditioners for parallely distributed linear equation systems

\[K u = f,\]

typically arising from the discretization of partial differential equations.

Main features of FROSch

Algebraic construction of two-level Schwarz preconditioners

One-level additive Schwarz preconditioners with exact solvers are of the form

\[M_{\rm OS-1}^{-1} = \sum\limits_{i=1}^N R_i^T K_i^{-1} R_i,\]

where the \(K_i = R_i K R_i^T\) correspond to problems on local overlapping subdomains.

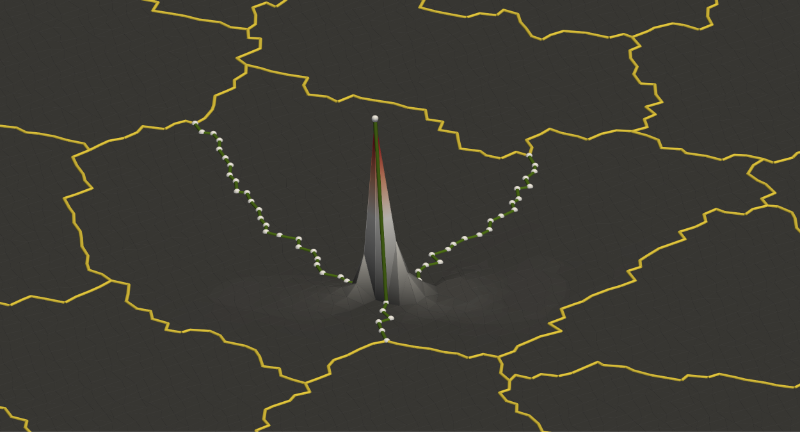
The \(R_i\) can be constructed in an algebraic fashion based the parallel distribution of the matrix \(K\) and the graph of the matrix \(K\). This preconditioner is not scalable, i.e., the condition number preconditioned operatpr \(M_{\rm OS-1}^{-1} K\) typically depends on the number of subdomains:

\[\kappa (M_{\rm OS-1}^{-1} K) \leq C \left( 1+ \frac{1}{H \delta} \right),\]

where \(\delta\) is the width of the overlap.

Adding a a suitable coarse level results in a scalable two-level Schwarz preconditioner

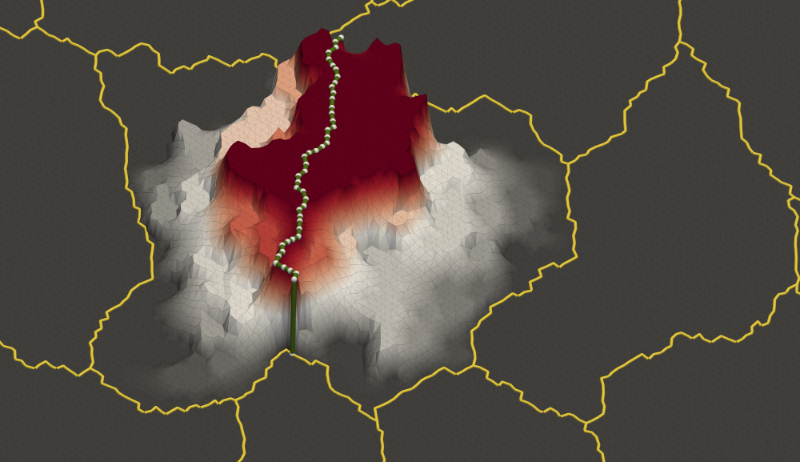
\[M_{\rm OS-2}^{-1} = \Phi K_0 \Phi^T + \sum\limits_{i=1}^N R_i^T K_i^{-1} R_i,\]

where the coarse matrix \(K_0 = \Phi^T K \Phi\) is computed as an RAP-product and \(\Phi\) is a matrix consisting of the coarse basis functions. In FROSch, the coarse basis functions \(\Phi\) are constructed in an algebraic fashion from the parallel distributed system matrix \(K\).

The main ingredients are a partition of unity on the interface of the non-overlapping domain decomposition, the nullspace of the operator, and discrete harmonic exntensions of the former two into the interior; see, e.g., GDSW (Generalized Dryja-Smith-Widlund) basis functions below.

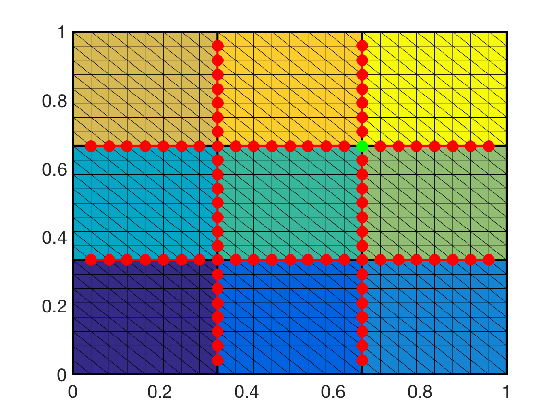
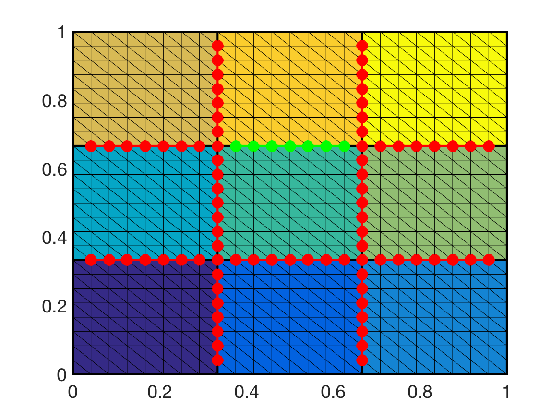
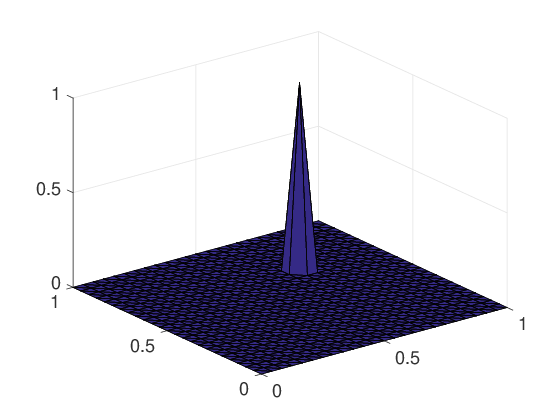
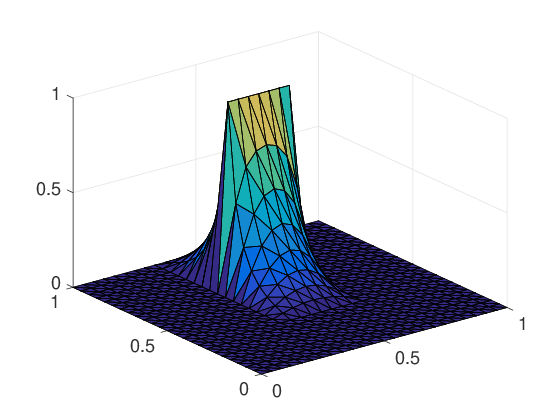
For example, the two-level Schwarz preconditioner with GDSW coarse space is scalable with a condition number bound independent of the number of subdomains:

\[\kappa \left(M_{\rm GDSW}^{-1} K \right) \leq \ C \left(1+\frac{H}{\delta}\right) \left( 1 + \log\left(\frac{H}{h}\right)\right)^{2}\]

References

 

Domain decomposition methods---algorithms and theory. Andrea Toselli and Olof Widlund, volume 34 of Springer Series in Computational Mathematics. Springer-Verlag, Berlin, 2005. [ bib ]

 

A family of energy minimizing coarse spaces for overlapping Schwarz preconditioners. Clark R. Dohrmann, Axel Klawonn, and Olof B. Widlund. In Domain decomposition methods in science and engineering XVII, volume 60 of Lect. Notes Comput. Sci. Eng., pages 247--254. Springer, Berlin, 2008. [ bib ]

 

Domain decomposition for less regular subdomains: overlapping Schwarz in two dimensions. Clark R. Dohrmann, Axel Klawonn, and Olof B. Widlund. SIAM J. Numer. Anal., 46(4):2153--2168, 2008. [ bib ]

 

Hybrid domain decomposition algorithms for compressible and almost incompressible elasticity. Clark R. Dohrmann and Olof B. Widlund. Internat. J. Numer. Methods Engrg., 82(2):157--183, 2010. [ bib ]

 

A parallel implementation of a two-level overlapping Schwarz method with energy-minimizing coarse space based on Trilinos. Alexander Heinlein, Axel Klawonn, and Oliver Rheinbach. SIAM J. Sci. Comput., 38(6):C713--C747, 2016. [ bib | DOI ]

Additive and multiplicative combination of Schwarz preconditioners

Schwarz preconditioners can be easily combined using the concept of Schwarz operators. In particular, Schwarz operators are projections of the form

\[P_{S} = M_{S}^{-1} K,\]

where \(M_{S}^{-1}\) is the corresponding Schwarz preconditioner. Schwarz preconditioners can be combined in an additive and multiplicative way. Given Schwarz operators \(P_0, ..., P_N\), the additive combination also results in a Schwarz operator

\[P_{\rm ad} = \sum\limits_{i=0}^{N} P_i.\]

Similarly, the Schwarz operators can be combined in a multiplicative,

\[P_{\rm mu} = I - (I - P_N) (I - P_{N-1}) \cdots (I - P_0),\]

and a symmetric multiplicative,

\[P_{\rm mu-sym} = I - (I - P_0) \cdots (I - P_{N-1}) (I - P_N) (I - P_{N-1}) \cdots (I - P_0),\]

way.

If \(P_1, ..., P_N\) correspond to overlapping subdomains (first level) while \(P_0\) corresponds to the coarse level, they can be combined in a hybird way:

\[P_{\rm hy-1} = I - \left( I - P_0 \right) \left( I - \sum\limits_{i=0}^{N} P_i \right) \left( I - P_0 \right) \\ P_{\rm hy-2} = \alpha P_0 + I - (I - P_N) \cdots (I - P_1)\]

References

 

Domain decomposition methods---algorithms and theory. Andrea Toselli and Olof Widlund, volume 34 of Springer Series in Computational Mathematics. Springer-Verlag, Berlin, 2005. [ bib ]

 

A family of energy minimizing coarse spaces for overlapping Schwarz preconditioners. Clark R. Dohrmann, Axel Klawonn, and Olof B. Widlund. In Domain decomposition methods in science and engineering XVII, volume 60 of Lect. Notes Comput. Sci. Eng., pages 247--254. Springer, Berlin, 2008. [ bib ]

 

Domain decomposition for less regular subdomains: overlapping Schwarz in two dimensions. Clark R. Dohrmann, Axel Klawonn, and Olof B. Widlund. SIAM J. Numer. Anal., 46(4):2153--2168, 2008. [ bib ]

 

Hybrid domain decomposition algorithms for compressible and almost incompressible elasticity. Clark R. Dohrmann and Olof B. Widlund. Internat. J. Numer. Methods Engrg., 82(2):157--183, 2010. [ bib ]

 

A parallel implementation of a two-level overlapping Schwarz method with energy-minimizing coarse space based on Trilinos. Alexander Heinlein, Axel Klawonn, and Oliver Rheinbach. SIAM J. Sci. Comput., 38(6):C713--C747, 2016. [ bib | DOI ]

Implementation based on Xpetra

Xpetra enables the use of both Trilinos linear algebra frameworks, Epetra and Tpetra.

FROSch now supports the Kokkos programming model though the use of Tpetra. The FROSch library can therefore profit from the efforts of the Kokkos package to obtain performance portability by template meta-programming, also on modern hybrid architectures with accelerators.

Simple user interface

FROSch provides a simple user interface. Therefore, the standard GDSW preconditioner can be constructed within a few lines from the fully assembled parallel distributed matrix K and a list of parameters ParameterList:

typedef KokkosClassic::DefaultNode::DefaultNodeType Node;
typedef FROSch::GDSWPreconditioner<double,int,long long,Node> FROSchGDSW;

Teuchos::RCP<FROSchGDSW> Prec(new FROSchGDSW(K,ParameterList);

Prec->initialize(Dimension,OL,RepeatedMap);

Prec->compute();

In addition to that, FROSch provides a Stratimikos interface and can therefore be called through the Thyra framework.

(click for more information)

Applications

FROSch has already been used in different applications, such as

• structural mechanics simulations,
• Computational Fluid Dynamics (CFD) simulations, and
• multi-physics simulations, e.g., Fluid-Structure Interaction (FSI) simulations.

See also Projects.